KMP算法分析

KMP算法是字符串匹配中的经典算法。相比暴力匹配算法的时间复杂度为O(m*n)，KMP算法的时间复杂度为O(m+n)。虽然，之后又出现了比KMP算法还高效的字符匹配算法，不过KMP算法作为经典，一直作为算法学习中的教材知识。 KMP算法流程: 假设现在文本串S匹配到 i 位置，模式串P匹配到 j 位置

如果j = -1，或者当前字符匹配成功（即S[i] == P[j]），都令i++，j++，继续匹配下一个字符；

如果j != -1，且当前字符匹配失败（即S[i] != P[j]），则令 i 不变，j = next[j]。此举意味着失配时，模式串P相对于文本串S向右移动了j - next [j] 位。

换言之，当匹配失败时，模式串向右移动的位数为：失配字符所在位置 - 失配字符对应的next 值（next 数组的求解会在下文的3.3.3节中详细阐述），即移动的实际位数为：j - next[j]，且此值大于等于1。

很快，你也会意识到next 数组各值的含义：代表当前字符之前的字符串中，有多大长度的相同前缀后缀。例如如果next [j] = k，代表j 之前的字符串中有最大长度为k 的相同前缀后缀。

此也意味着在某个字符失配时，该字符对应的next 值会告诉你下一步匹配中，模式串应该跳到哪个位置（跳到next [j] 的位置）。如果next [j] 等于0或-1，则跳到模式串的开头字符，若next [j] = k 且 k > 0，代表下次匹配跳到j 之前的某个字符，而不是跳到开头，且具体跳过了k 个字符。

代码:

int KmpSearch(char* s, char* p)
{
  int i = 0;
  int j = 0;
  int sLen = strlen(s);
  int pLen = strlen(p);
  while (i < sLen && j < pLen)
  {
    if (j == -1 || s[i] == p[j])
    {
      i++;
      j++;
    }
    else
    {
      j = next[j];
    }
  }
  if (j == pLen)
    return i - j;
  else
    return -1;
}

KMP算法的核心步骤就是准备好next[j]数组了。也是KMP算法难点之处。 KMP算法和暴力算法的区别之处在于:暴力算法在模式串匹配失败的时候,下一个字符的匹配，模式串的索引会变为0，从头开始匹配并且字符串的i索引会往回撤，再从下一位开始匹配(i = i - j + 1)使得前面匹配的索引移动对下一个字符的匹配没有用处。而KMP算法就是利用了前面匹配的结果。字符串索引i不会往回退，只会往后走。而模式串根据next[]数组中存的值，用相应的索引值和下一个字符进行匹配。

关于next[j]数组的求法，涉及到了模式串每个对应字符的前后缀最长公共元素的长度。 next[]数组其实就是模式串前缀后缀最长公共元素长度值整体往右移动一位，比如next[2]存的是p[3]的前缀后缀最长公共元素长度值。next[0]初始为-1，并且p[last]的前缀后缀最长公共元素长度值不需要求，因为到最后一位说明匹配成功了。

kmp

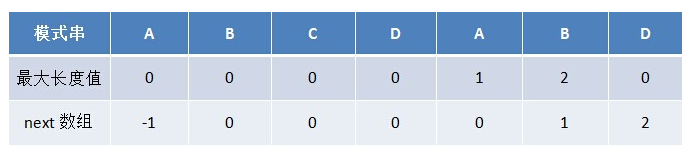
next数组的值是根据递推计算得出来的。代码：

void GetNext(char* p,int next[])  
{  
    int pLen = strlen(p);  
    next[0] = -1;  
    int k = -1;  
    int j = 0;  
    while (j < pLen - 1)  
    {  
        //p[k]表示前缀，p[j]表示后缀  
        if (k == -1 || p[j] == p[k])   
        {  
            ++k;  
            ++j;  
            next[j] = k;  
        }  
        else   
        {  
            k = next[k];  
        }  
    }  
}  

next数组值的优化:

//优化过后的next 数组求法  
void GetNextval(char* p, int next[])  
{  
    int pLen = strlen(p);  
    next[0] = -1;  
    int k = -1;  
    int j = 0;  
    while (j < pLen - 1)  
    {  
        //p[k]表示前缀，p[j]表示后缀    
        if (k == -1 || p[j] == p[k])  
        {  
            ++j;  
            ++k;  
            //较之前next数组求法，改动在下面4行  
            if (p[j] != p[k])  
                next[j] = k;   //之前只有这一行  
            else  
                //因为不能出现p[j] = p[ next[j ]]，所以当出现时需要继续递归，k = next[k] = next[next[k]]  
                next[j] = next[k];  
        }  
        else  
        {  
            k = next[k];  
        }  
    }  
}  

参考文章:

http://blog.csdn.net/v_july_v/article/details/7041827

Minimalist Life

KMP算法分析

Search

Table of Contents